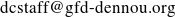
準備: NCEP 再解析の東西風 uwnd.2010JanFeb.nc の日平均値データ *1 を適当な作業ディレクトリにダウンロードし,そこに cd します.
Rubyでは既存のクラスに,メソッド等を追加したり再定義することが簡単にできます. このため,GPhys にない機能を簡単に付け加えて利用できます.
GPhys クラスは,NumRu というモジュール内に定義されています.これを拡張,再定義するには,まず, numru/gphys を require し (あるいは,描画も行う場合は numru/ggraph を require し -- ∵ numru/ggraph は内部で numru/gphys を require する), 次のように続けます(途中に無関係なコードをはさんでも構いません). ここで, ... には,メソッド定義等を書きます.
module NumRu
class GPhys
...
end
end
メソッドを追加するサンプルプログラムを示しますす:
サンプルプログラム variance.rb:
require "numru/ggraph"
iws = (ARGV[0] || 1).to_i
module NumRu
class GPhys
def variance(*dims)
dev = self - self.mean(*dims)
variance = (dev**2).mean(*dims)
variance.long_name = "variance: "+long_name if variance.is_a?(GPhys)
variance
end
end
end
include NumRu
u = GPhys::IO.open("uwnd.2010JanFeb.nc","uwnd")[false,{0..30,3}] # Jan 1,4,..,31
p "variance (all data points):",u.variance
DCL.swpset('iwidth',900)
DCL.swpset('iheight',450)
DCL.swpset('ldump',true) if iws==4
DCL.gropn(iws)
DCL.sldiv('y',2,1)
DCL.sgpset('isub', 96) # control character of subscription: '_' --> '`'
DCL.glpset('lmiss',true)
GGraph.set_fig "itr"=>2, "viewport"=>[0.15,0.75,0.2,0.8]
GGraph.tone u.variance(0).mean(-1), true, "int"=>50
GGraph.color_bar
GGraph.set_fig "itr"=>10, "viewport"=>[0.05,0.8,0.2,0.8]
GGraph.set_map "coast_world"=>true
GGraph.tone u.cut("level"=>850..200).variance("level").mean("time")
GGraph.color_bar
DCL.grcls
実行結果
標準出力(一部):
"variance (all data points):" 260.16754165344 m2 s-2
図: (full size) :

上の例ではバリアンスを計算するメソッド variance を定義しました.
def variance(*dims) という形で定義しているので,任意個の引数をとることができます.
それは,
dev = self - self.mean(*dims) variance = (dev**2).mean(*dims)
において,mean というメソッドにそのまま引き継がれます.
mean は,対象となる GPhys オブジェクトの次元を任意個,名前または番号で(ゼロ以上の整数で前から,負の整数で後ろから)指定すると,それらの次元に沿った平均を返すメソッドです.
引数がない場合は,すべてのデータ点を使った平均をスカラー値 (単位付きの数値 UNumeric)
で返します.
今回定義した variance は,この柔軟性をそのまま引き継ぎます.
なお,mean は格子点の間隔を考慮しない単純平均です (ただし,データ欠損は除いてカウントします) ので,
不等間隔なデータに適用する場合はその点を意識しておく必要があります.格子点間隔を考慮する平均には
average があります.
データ処理をメソッドして定義しておくと,それをさらに別のメソッドに引き継ぐ「メソッドチェーン」で使える利点があります.上の例では,図示する際には次のように時間平均をとってます:
GGraph.tone u.cut("level"=>850..200).variance("level").mean("time")
準備: NCEP 再解析の東西風 uwnd.2010JanFeb.nc の日平均値データ *2 を適当な作業ディレクトリにダウンロードし,そこに cd します.
スペクトル解析を行う場合を考えてみましょう.フーリエ変換では実空間から波数空間に移行するので,座標軸の変更は必須です.GPhysにはフーリエ解析ライブラリが含まれていますが,gphys_fft.rb という独立したファイルに格納されており,まさに前節で述べたGPhys追加定義と同じ形になっています.従って,このファイルは座標の更新を必要とする拡張の一サンプルファイルとしてみることができます.ソースコードは,GPhys のソースファイルを展開したトップディレクトリの下,または GPhys インストール先トップディレクトリの下の, lib/numru/gphys/gphys_fft.rb というパスにあります.
さて,gphys_fft.rb の座標軸更新は大掛かりな例ですので,あまりとっつきやすくないかもしれません.そこで,もっと簡単な例として,差分法で微分を評価するメソッドを追加する例を示します.
サンプルプログラム deriv.rb:
require "numru/ggraph"
iws = (ARGV[0] || 1).to_i
module NumRu
class GPhys
def deriv(dim)
dim = dim_index(dim) # input dim can be a String or an Integer
x = axis(dim).to_gphys
a = [true]*dim + [1..-1,false]
b = [true]*dim + [0..-2,false]
dydx = ( self[*a] - self[*b] ) / ( x[1..-1] - x[0..-2] )
xi = ( x[1..-1] + x[0..-2] ) / 2
dydx.axis(dim).set_pos(xi.coord(0))
dydx.long_name = "d #{name}/d #{x.name}"
dydx
end
end
end
include NumRu
u = GPhys::IO.open("uwnd.2010JanFeb.nc","uwnd")[false,0].cut("lon"=>140)
ushear_p = u.deriv("level")
H = UNumeric[8e3,"m"]
z = -H * ( u.axis("level").pos / 1000.0 ).log
z.name = "z"
z.long_name = "log-p height"
z.set_att("positive","up")
u.axis("level").set_pos(z)
ushear_z = u.deriv(-1)
DCL.swpset('iwidth',800)
DCL.swpset('iheight',400)
DCL.swpset('ldump',true) if iws==4
DCL.gropn(iws)
DCL.sldiv('y',2,1)
DCL.sgpset('isub', 96) # control character of subscription: '_' --> '`'
DCL.glpset('lmiss',true)
GGraph.set_fig "itr"=>2, "viewport"=>[0.15,0.75,0.2,0.8]
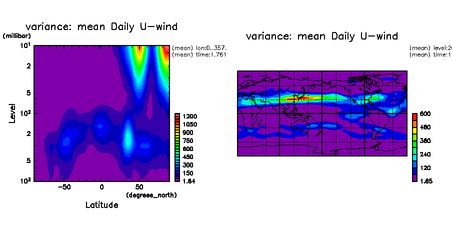
GGraph.tone_and_contour ushear_p
GGraph.color_bar
GGraph.set_fig "itr"=>1
GGraph.tone_and_contour ushear_z
GGraph.color_bar
DCL.grcls
実行結果
図: (full size) :
この例では,deriv というメソッドを定義しています.
このメソッドは,番号または名前で指定された次元に沿って,隣り合う格子点値をもとに差分を評価します.その際,結果の座標を両者の中央に設定することで,中央差分となるようになっています.
deriv の内容を順を追って説明します.
dim = dim_index(dim) # input dim can be a String or an Integer
では,該当する次元の番号を取得します.入力が文字列であれば次元名と判断して番号 (0,1,..) を返します.また,入力が負の整数であれば,後ろからの指定であるとみなし,0,1,.. の番号に換算します.
x = axis(dim).to_gphys
ここでは,dim 版目の座標軸をとり,to_gphys で主座標変数 (格子点の座標値を収める1次元 VArray) を主変数(データ値)とする GPhys にしています(つまり x は一次元で,主変数と1次元目の主座標変数が一致します).ここで GPhys にする理由は,あとで多次元データとの商を計算するためです.GPhys どうしの計算であれば,次元の対応づけが名前ベースで自動的に行われるので,多次元対一次元の演算が可能なのです.
a = [true]*dim + [1..-1,false] b = [true]*dim + [0..-2,false] dydx = ( self[*a] - self[*b] ) / ( x[1..-1] - x[0..-2] )
ここでは,たとえば dim が 2 であれば,a は [true,true,1..-1,false], b は [true,true,0..-2,false] となります.よって,self[*a] は3番目の次元について,2番目の要素から最後の要素までをとったサブセット,self[*b] は3番目の次元について,先頭の要素から,後ろから2番目の要素までをとったサブセットとなります. 従って,dydx は dim 軸に沿って隣あう格子点間でとった差分になるのです.
しかし,このままでは,dydx の dim 軸は,演算左辺の self[*a] のそれと同じままです.GPhys の2項演算では座標は左辺から引き継ぐ仕様になっているからです.このままでも後退差分としてはよいのですが,中央差分とすべく格子の位置を中央にもっていきます.それが以下です.
xi = ( x[1..-1] + x[0..-2] ) / 2 dydx.axis(dim).set_pos(xi.coord(0))
ここでは xi.coord(0) (最初の軸の主座標変数)とするかわりに xi.data (主変数)としても同じです.あとは仕上げです.
dydx.long_name = "d #{name}/d #{x.name}"
では記述的な名前を表す予約属性 "long_name" つけかえます(ここで name を使うのが適切とは限りませんが,long_name より簡潔であることを期待してます.汎用メソッドしてはあまりよくないかもしれません).
以上でメソッド deriv の説明が終わりました.次はその利用について,簡単に説明します.
上のサンプルプログラムでは,まずはもともとの鉛直座標軸(気圧;名前は(なぜか)level)について,差分をとります;
ushear_p = u.deriv("level")
ついで,今度は鉛直座標を圧力対数座標にしたうえで,差分をとります.座標入れ替えは,
u.axis("level").set_pos(z)
で行われますが,u という GPhys オブジェクトにおける座標軸を取り替えているだけなので,もとのファイルには影響を及ぼしません.(もとのファイルも書き換える方法もありますが,デフォルトではファイルは読み込みのみの書き出し禁止でオープンされます).よって,次に鉛直座標で微分すると圧力対数座標での微分となります.
(すみません,未作成です.)
*1このデータはNOAAのサイトから取得しました.本ファイルには1-2月のデータのみ入ってます.
*2このデータはNOAAのサイトから取得しました.本ファイルには1-2月のデータのみ入ってます.