

平均の計算をおこなうルーチン avr.f90 の動作をテストする. 具体的には
をチェックする.
ここでは物理量の分布として与える関数をいろいろ変えて平均の計算をテストする. 元の分布, 平均をとった後の分布、および絶対誤差の図を描いてみる.
| テスト番号 | 変数名 | テストする関数 | 物理量の分布 | 境界条件 | Update |
| テスト 11 | w | w_avr_s( s_avr_w(w) ) を 30 回繰り返す | w = sin(2πx/Lx) sin(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/21 |
| テスト 10 | w | w_avr_s( s_avr_w(w) ) を 5 回繰り返す | w = sin(2πx/Lx) sin(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/21 |
| テスト 9 | w | w_avr_s( s_avr_w(w) ) | w = sin(2πx/Lx) sin(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/21 |
| テスト 8 | u | u_avr_s( s_avr_u(u) ) を 30 回繰り返す | u = cos(2πx/Lx) cos(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/21 |
| テスト 7 | u | u_avr_s( s_avr_u(u) ) を 30 回繰り返す | u = sin(2πx/Lx) sin(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/21 |
| テスト 6 | u | u_avr_s( s_avr_u(u) ) を 5 回繰り返す | u = cos(2πx/Lx) cos(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/20 |
| テスト 5 | u | u_avr_s( s_avr_u(u) ) | u = cos(2πx/Lx) cos(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/20 |
| テスト 4 | u | u_avr_s( s_avr_u(u) ) を 5 回繰り返す | u = sin(2πx/Lx) sin(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/20 |
| テスト 3 | u | u_avr_s( s_avr_u(u) ) | u = sin(2πx/Lx) sin(2πz/Lz) | x: 周期, z:固定壁 | 2004/09/20 |
| テスト 2 | u | u_avr_s( s_avr_u(u) ) | u = cos(πx/Lx) cos(πz/Lz) | 2004/09/03 | |
| テスト 1 | u | u_avr_s( s_avr_u(u) ) | u = sin(πx/Lx) sin(πz/Lz) | 2004/09/03 |
| テストする関数 | w_avr_w( s_avr_w(w) ) を 30 回繰り返す |
| 物理量の分布 | w = sin(2πx/Lx) sin(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
 |
 |
 |
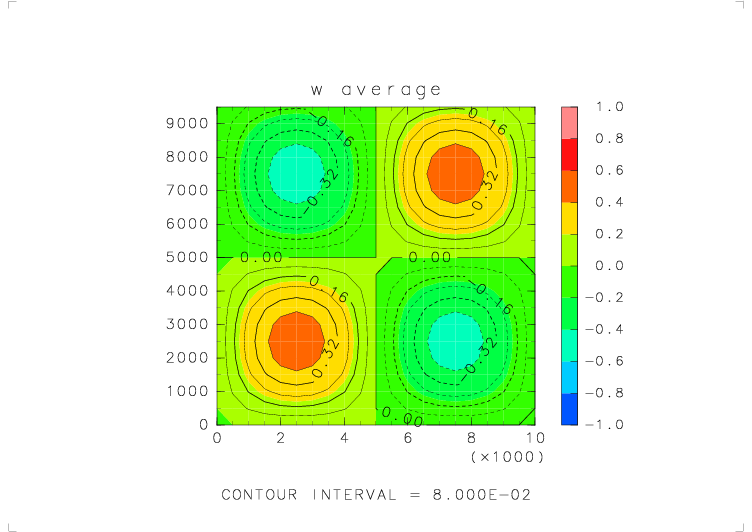
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | w_avr_w( s_avr_w(w) ) を 5 回繰り返す |
| 物理量の分布 | w = sin(2πx/Lx) sin(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
 |
 |
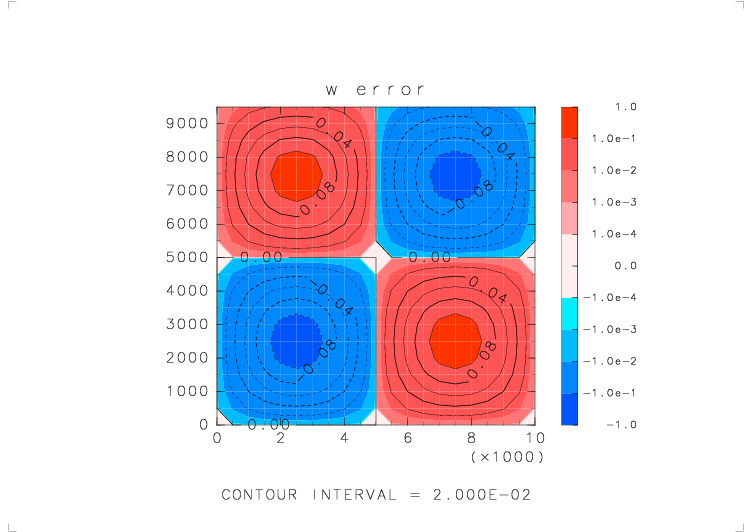 |
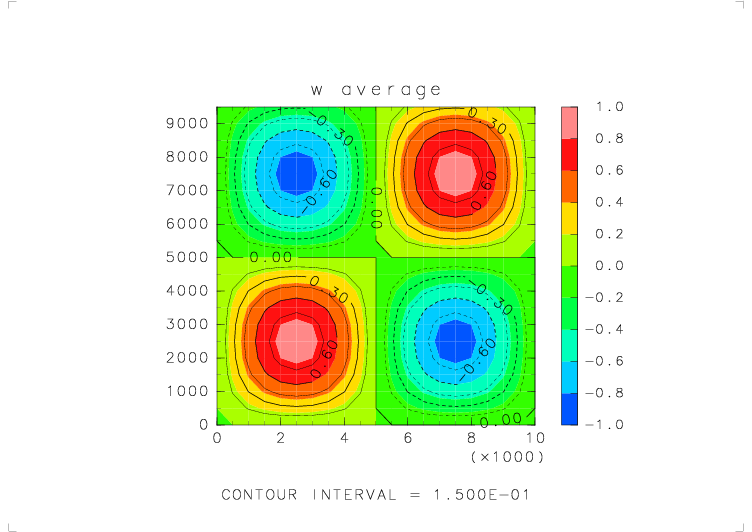
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | w_avr_w( s_avr_w(w) ) |
| 物理量の分布 | w = sin(2πx/Lx) sin(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
 |
 |
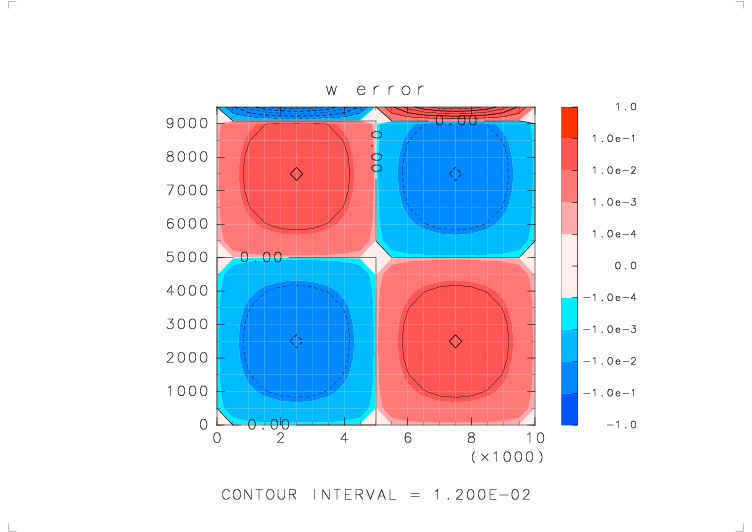 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | u_avr_s( s_avr_u(u) ) を 30 回繰り返したもの |
| 物理量の分布 | u = cos(2πx/Lx) cos(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
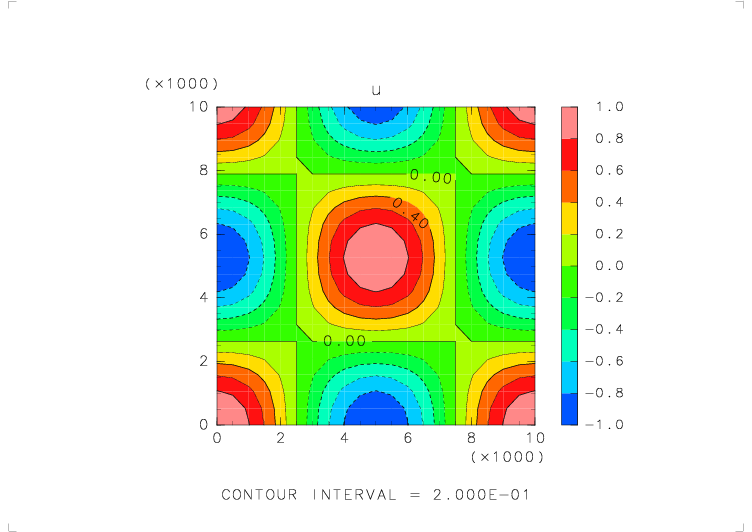 |
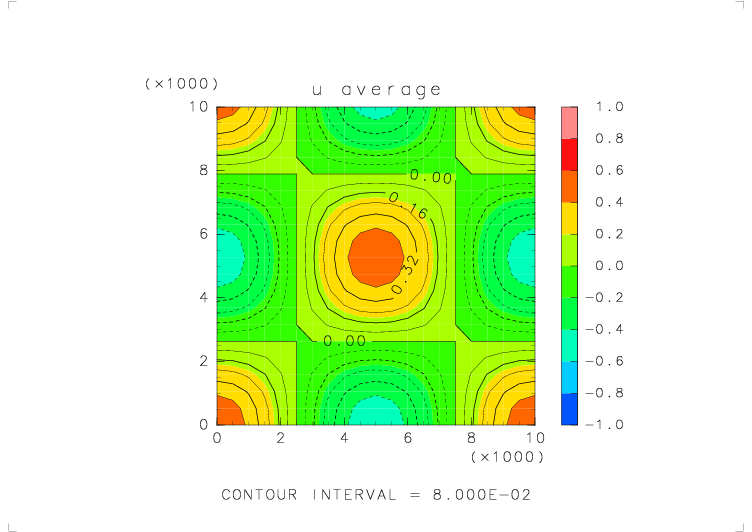 |
 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | u_avr_s( s_avr_u(u) ) を 30 回繰り返したもの |
| 物理量の分布 | u = sin(2πx/Lx) sin(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
 |
 |
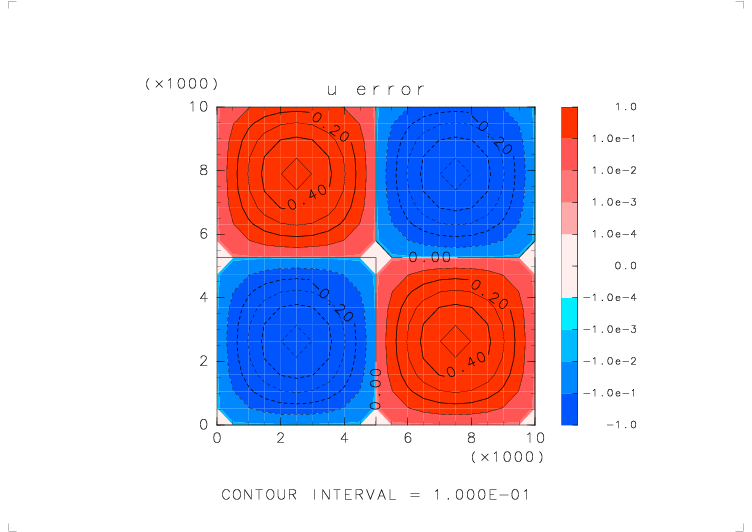 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | u_avr_s( s_avr_u(u) ) を 5 回繰り返したもの |
| 物理量の分布 | u = cos(2πx/Lx) cos(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
 |
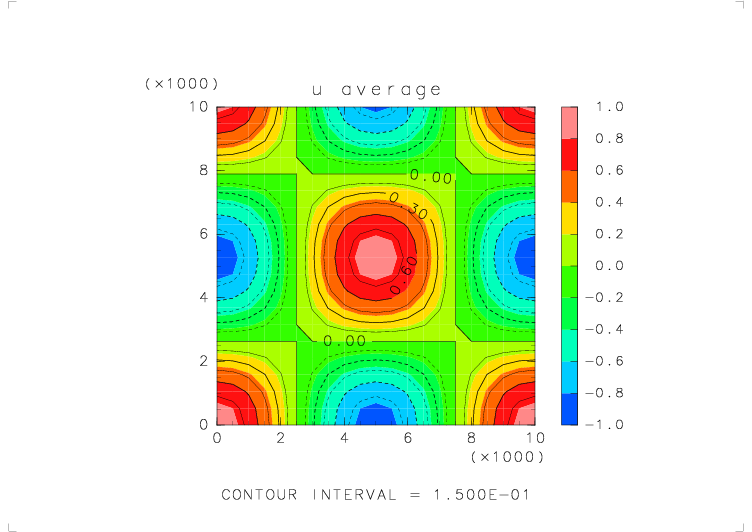 |
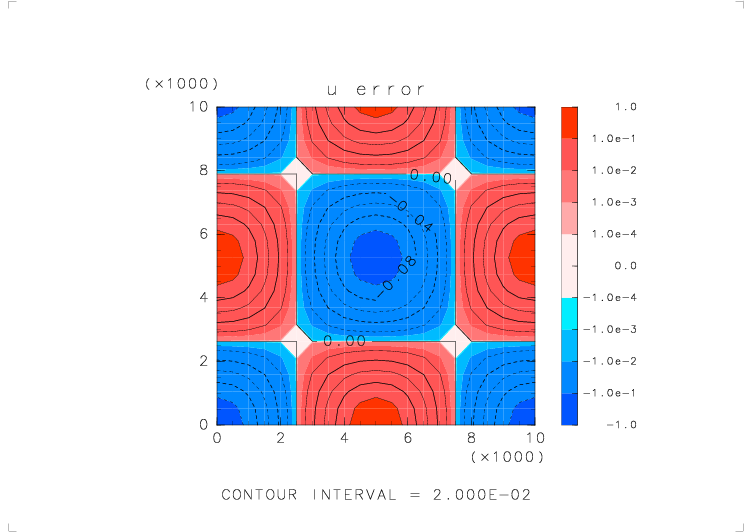 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
繰り返し平均をとっても分布の形が一定の方向にずれていくことはない.
| テストする関数 | u_avr_s( s_avr_u(u) ) |
| 物理量の分布 | u = cos(2πx/Lx) cos(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
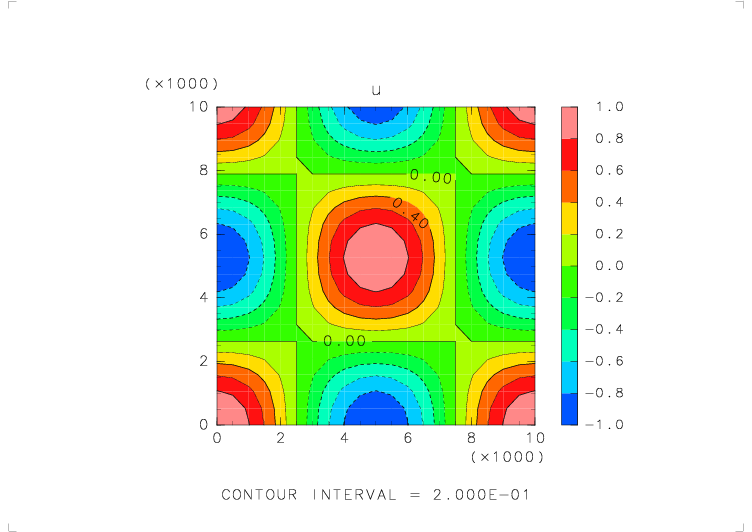 |
 |
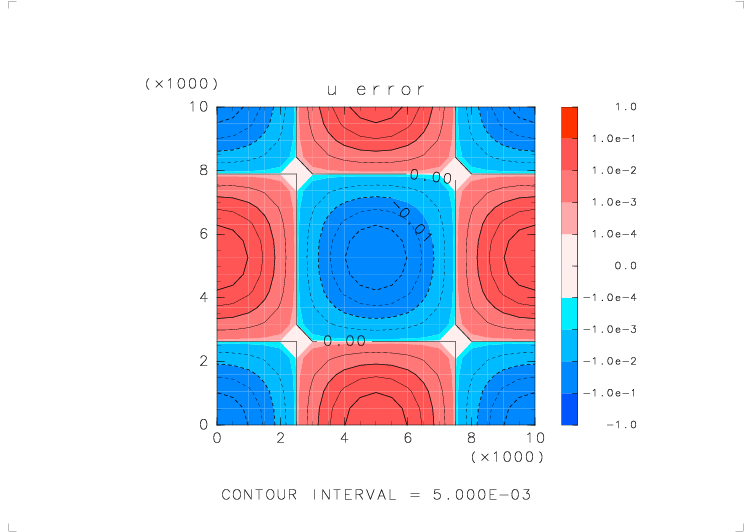 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | u_avr_s( s_avr_u(u) ) を 5 回繰り返したもの |
| 物理量の分布 | u = sin(2πx/Lx) sin(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
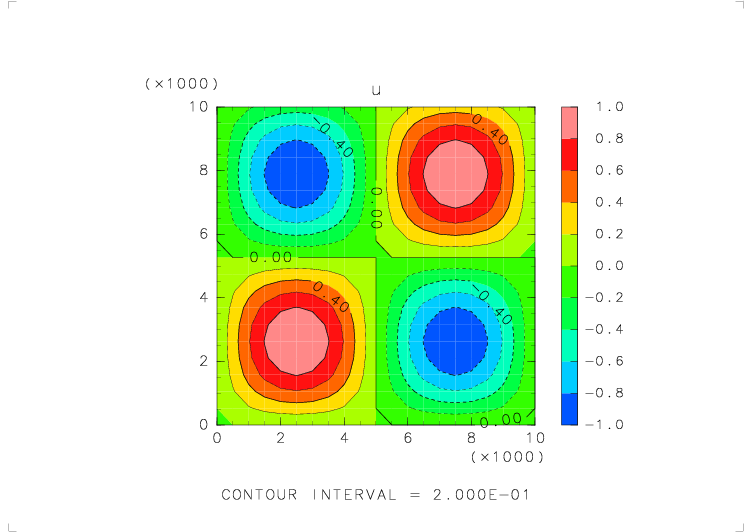 |
 |
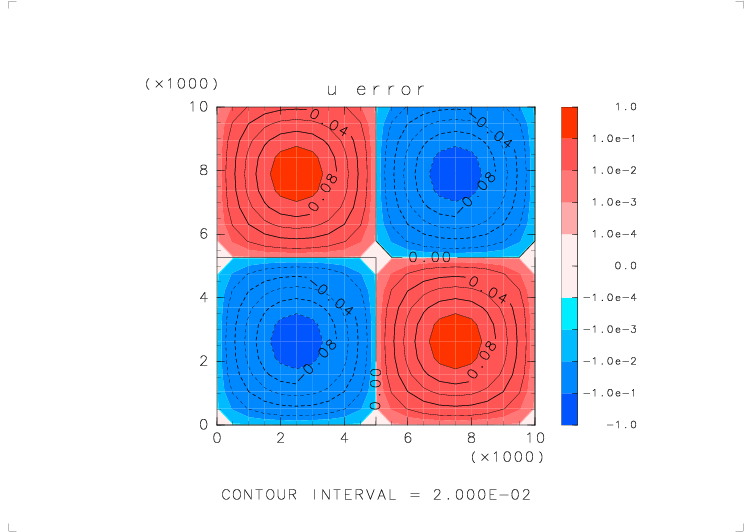 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
繰り返し平均をとっても分布がずれることはない.
| テストする関数 | u_avr_s( s_avr_u(u) ) |
| 物理量の分布 | u = sin(2πx/Lx) sin(2πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
| 境界条件 | x: 周期境界, z: 固定壁 |
 |
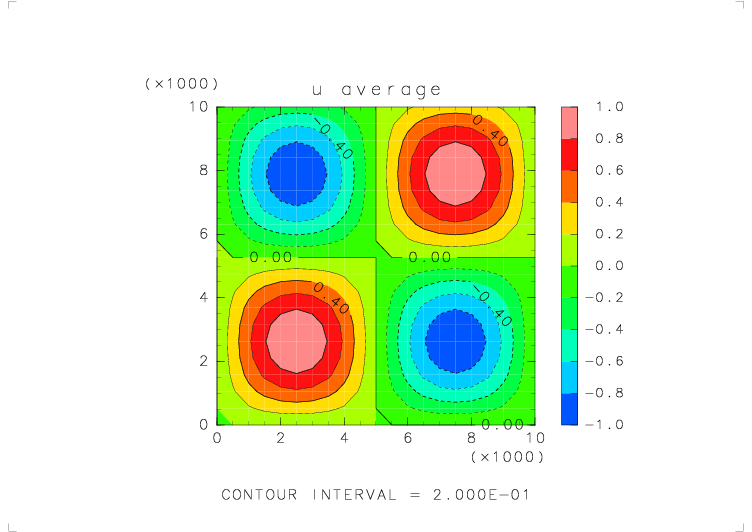 |
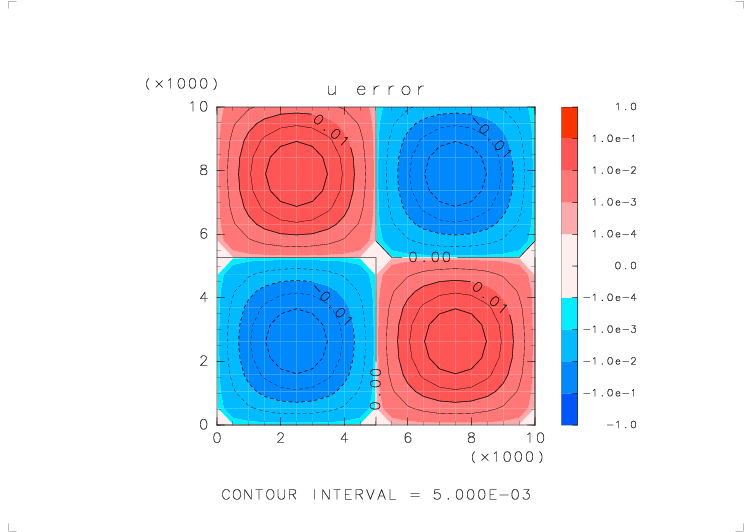 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での誤差 |
| テストする関数 | u_avr_s( s_avr_u(u) ) |
| 物理量の分布 | u = sin(πx/Lx) sin(πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
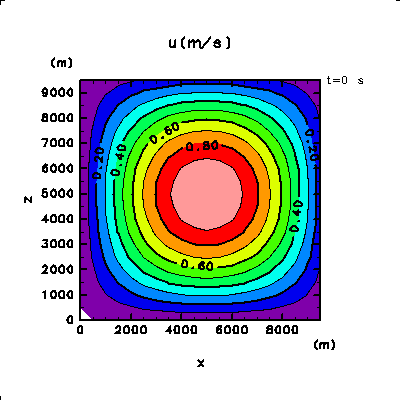 |
 |
 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での相対誤差の対数表示 |
平均をとる前と後の図を見比べると概ねよさそうに見える.
内部領域では 10^(-5) 以下の誤差.
境界付近では物理量が 0 に近いから値がずれているのだろうか ?
原点が白くなっているのは何故 ?
| テストする関数 | u_avr_s( s_avr_u(u) ) |
| 物理量の分布 | u = cos(πx/Lx) cos(πz/Lz) (Lx, Lz : x, z 方向の領域の幅) |
 |
 |
 |
| 元の関数の分布 | 平均をとった後の分布 | 平均をとる前と後での相対誤差を対数表示したもの |
側面境界で値が大きく異なっている. それ以外の領域では 10^(-5) 以下の誤差.