/地球流体セミナー
/講演資料一覧
/2005-09-12/
全球雲解像モデルの開発と計算例
富田 浩文 氏(地球環境フロンティア研究センター)
2005 年 9 月 12 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.
|
目次
|

|
動機(1)
- 一つ一つの雲を陽に表現する
- 「深い対流」は直接表現しよう
- MM5 などの雲解像モデルの全球版とする
|

|
動機(2)
- 目標解像度, 水平 5km 以下, 鉛直 数100m 以下
- スペクトル変換だと不利, Legendre 変換の計算量は N^3 に比例して増加.
- 球面一様格子はいろいろある
- 陰陽格子
- 立方体
- 正 8 面体
- カナダでやっているのは緯度経度格子点法
- ...
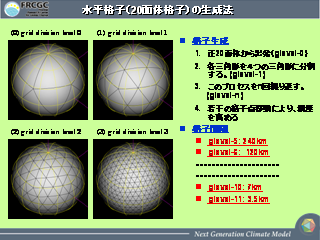
- 正 20 面体のメリット
- 起源をたどると 1950 年代の Williamson
- 一様な格子を作りやすい
- 等方的な格子を作りやすい
- 一つの格子が 6 角形になる
|

|
開発したモデル
|

|
開発メンバー
|
|
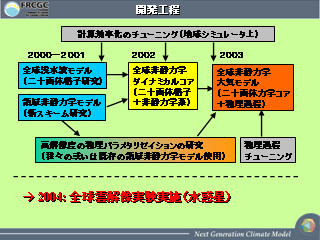
開発工程
|

|
現在の状況
- 鉛直座標は z で比例配分したような形.
- 里村さんは山の斜面に直行するように鉛直軸をとっているらしい.
- 実際には, 斜面の傾きが 45 度くらいでも NICAM の鉛直座標でも
結構いけてしまう
- 最近の傾向は step mountain として扱う方法
- 上層まで山の影響が出てしまうのを嫌う場合には, 山の高さにあわせて
変換関数を変えれば回避できる.
|
|
水平格子の生成法
|
|
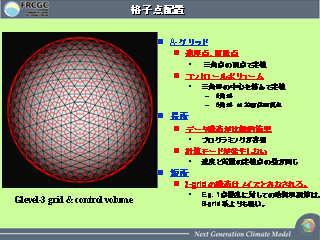
格子点配置
- A grid
- 6 角形のコントロールボリューム
- 速度点と質量点が同じ
-
- * B-grid みたいのを考えると, 速度点と質量点の数が違ってしまって
計算モードが発生する.
- 2-grid の構造はノイズみなされてしまう
ex) 地衡流調節: 奇数格子と偶数格子が de-couple してしまう.
|
|
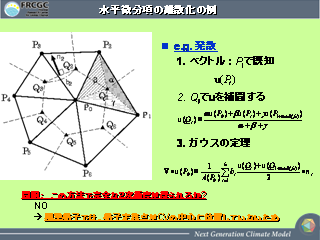
水平微分項の離散化の例
- 発散の計算方法
- 速度は各頂点で定義されている.
- 1 つの三角形の真中の点における速度は面積を使って補完
- 隣あう三角形にはさまれた辺の上の速度は両隣の三角形の真中の速度
を足して 2 で割って決める.
- そいつに normal vector かけて全部足す.
- 球面上の三角形は正三角形ではないため,
格子点が有限体積の中心に位置しない.
- このため離散化された発散が 2 次精度とならない
|
|
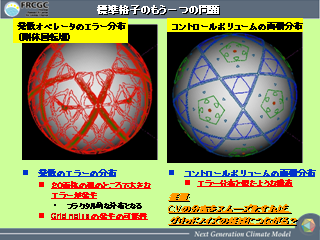
標準格子のもう一つの問題
- 剛体回転の流れを与えた場合の発散の誤差
- 20 面体の弧の部分で大きな誤差が現れる
- 発散の誤差分布や Control volume の分布がフラクタル構造になる
|
|
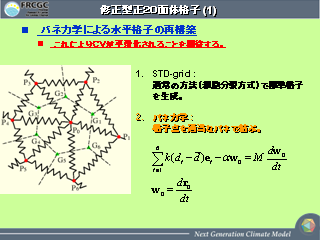
修正型正 20 面体格子(1)
- 格子点をバネで結んだ系を考えて平衡常態を解く.
- 無次元パラメータとしてバネの自然長を与える.
これが tuning parameter になる.
- 格子修正法は他にもいくつか提案されているらしい.
-
|

|
修正型正 20 面体格子(1): 格子生成の手順
|
|
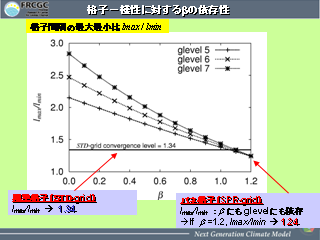
格子一様性に対するβの依存性
|
|
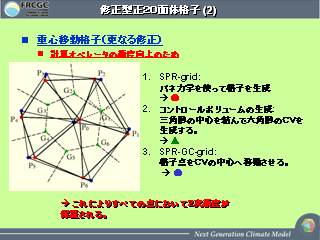
修正型正 20 面体格子(2)
- バネ力学を用いて求めた格子点が,
コントロールボリュームの重心に位置するように修正する.
- glevel-0 の格子点の位置を固定することで,
常に同じ格子点が得られるようにする.
|
|
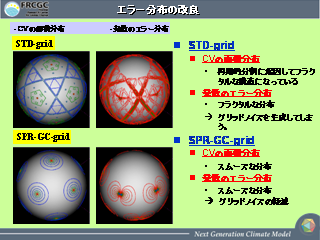
エラー分布の改良
- 剛体回転の流れを与えた場合の発散の誤差
- glevel-0 の格子点にエラーが残る
|
|
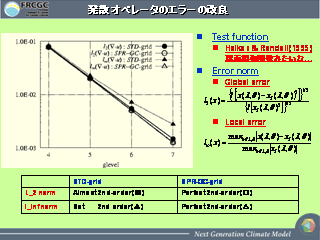
発散オペレータの改良
|

|
浅水モデルを用いた検証
|

|
Williamson (1992) の Test Case 2 (1)
|
|
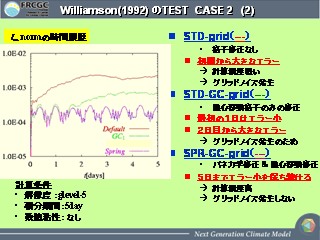
Williamson (1992) の Test Case 2 (2)
- L∞ノルムの振動は, 緯度方法に伝播する波数 0 の重力波
|
|
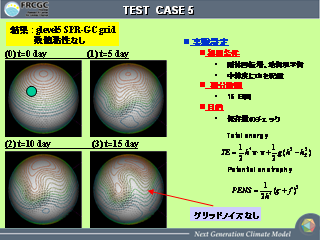
Test Case 5 (1)
|
|
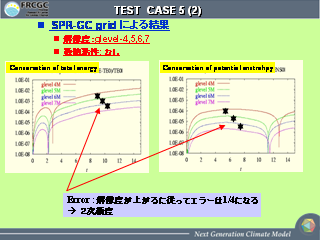
Test Case 5 (2)
|

|
非静力学モデリングの方針
- 浅い大気の近似を排除
- すべてのメトリック項とコリオリ項を扱う
|

|
支配方程式
|
|
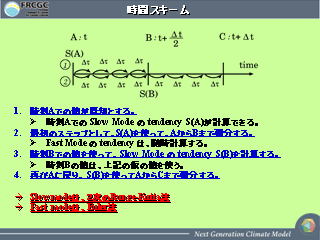
時間スキーム
|

|
Small Step での時間積分 (1)
- 水平方向の運動量は先に決める.
- 先に決めた量を使って, エネルギー方程式と W の式を連立させて
implicit に W は求める.
- P は total energy の式を時間積分して全エネルギーを求めて
それから, 内部エネルギーを求めて, P を決める.
|

|
Small Step での時間積分 (2)
|

|
Small Step での時間積分 (3)
|

|
Large Step での時間積分
|

|
Held and Suarez Dynamical Core 実験 (1)
|

|
Held and Suarez Dynamical Core 実験 (2)
|
|
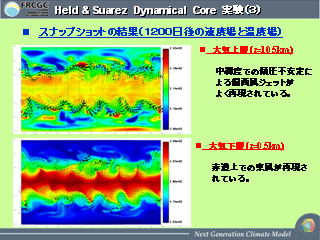
Held and Suarez Dynamical Core 実験 (3)
|
|
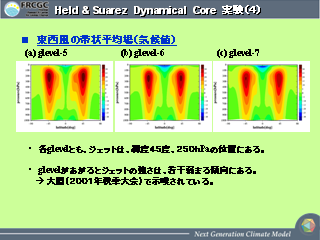
Held and Suarez Dynamical Core 実験 (4)
- 平均東西風
- glevel が上がるとジェットが若干弱まる傾向にある.
|
|
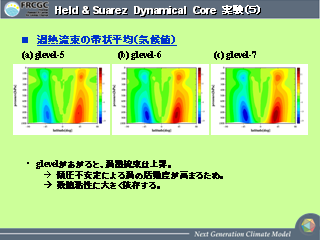
Held and Suarez Dynamical Core 実験 (5)
|

|
Held and Suarez Dynamical Core 実験 (6)
- 平均東西風のモデル比較
- GME: ドイツ気象局の 20 面体モデル
- IFS: ECMWF のスペクトルモデル
|

|
Held and Suarez Dynamical Core 実験 (7)
- 渦熱流束のモデル比較
- GME: ドイツ気象局の 20 面体モデル
- IFS: ECMWF のスペクトルモデル
|

|
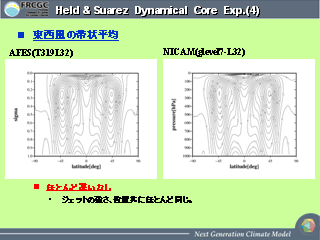
HSTC での AFES との比較 (1)
- AFES: CCSR/NIES AGCM を ES 用に最適化したモデル(スペクトルモデル).
|
|
HSTC での AFES との比較 (2)
|
|
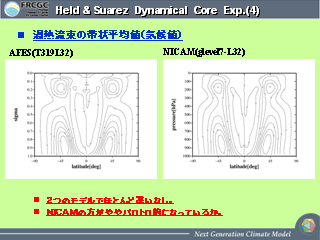
HSTC での AFES との比較 (2)
- 平均渦熱流束の比較
- NICAM はちょっと鉛直方向になまった分布をしている.
|
|
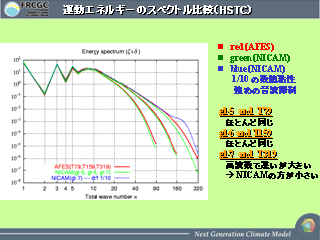
HSTC での AFES との比較: 運動エネルギースペクトル
- 解像度を高くすると高波数領域でのずれが大きくなる.
- 非静力学効果は現れない解像度と思っているが…
|
|
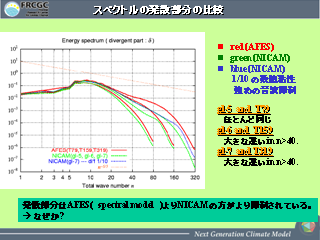
HSTC での AFES との比較: 運動エネルギースペクトル(発散成分のみ)
- 高波数領域でのずれがさらに大きくなる(NICAM の方が小さい).
- 重力波の伝播特性の違いによるものかもしれない.
|
|
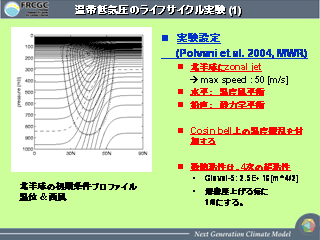
温帯低気圧のライフサイクル実験 (1)
|
|
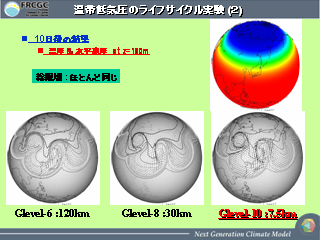
温帯低気圧のライフサイクル実験 (2)
|
|
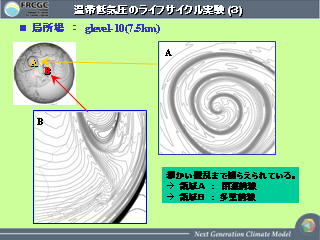
温帯低気圧のライフサイクル実験 (3)
|
|
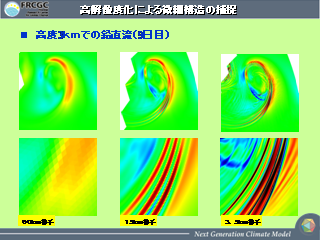
高解像度化による微細構造の捕捉
- 水平解像度を上げていくと, 前線の多重構造が現れるようになる.
|
|
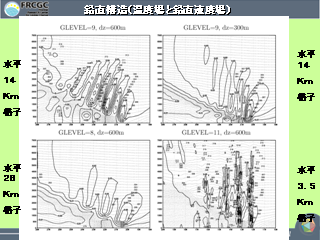
鉛直構造(温度場と鉛直速度場)
- 水平解像度を上げていくと, よりシャープな多重構造が現れる.
|
|
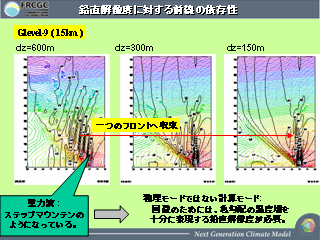
鉛直解像度に対する前線の依存性
- 鉛直格子を細かくすると多重前線は 1 つの前線に
収束
|

|
多重構造の模式図
- 2 つの要素
- 鉛直分解能が荒い場合, 温度差が階段状の山と同じ役割を果たす.
- 波源は不連続に分布, 隣り合う波源からの波が残ってしまう.
- 鉛直分解能が十分であれば, 波源は連続的に分布.
- 隣り合う格子点からの波は互いに打ち消し合い, 前線面は正しく表現される.
- 改善するには
- 下層の鉛直格子を段階的に細かくする
- 下部境界が free-slip であることも原因かもしれない
|

|
話の内容 (PartII)
|

|
物理過程の開発戦略
- いきなり数km 格子で試行錯誤できないので
-
- 地球の半径を小さくする: 6400km -> 640km
-
- 水平ストレッチ格子: 興味ある領域に格子を集める.
|

|
一部集中格子を用いる目的と方法
- CSIRO (McGregor)
- Canada: GEM unified model (Cote et al.)
|
|
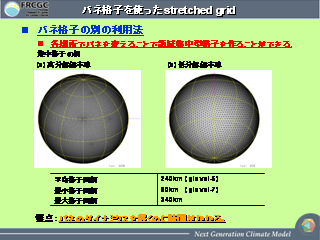
ばね格子を使った stretched 格子
- バネの自然長を場所によって変える
- 格子生成に時間がかかる
|

|
数学的な変換を使った stretched 格子
- 極に集中した格子を作成する
- 極付近では一様になるように,
変換関数の導関数は極付近で一定になるようにする.
- その格子を回転させる
|
|
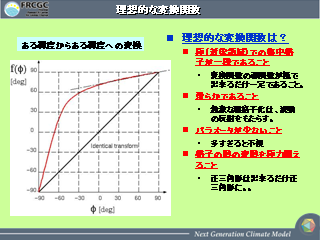
理想的な変換関数
|
|
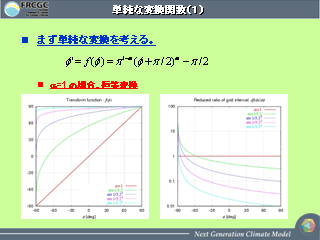
単純な変換関数 (1)
|

|
単純な変換関数 (2)
- 格子滑らか, 不連続はない.
- 赤道付近の格子は偏平になる.
|

|
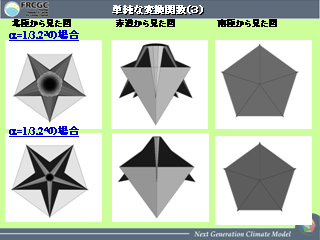
単純な変換関数 (2): だめな例その1
|
|
単純な変換関数 (3): だめな例その2
|
|
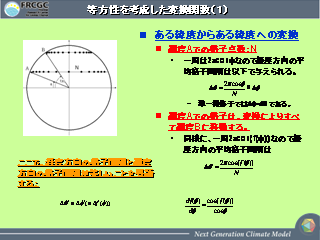
当方性を考慮した変換関数 (1)
- ある緯度円上の点は同じ緯度円に移るようにする.
- 等方性を考慮して, 緯度方向の格子間隔と経度方向の格子間隔が同じに
なるようにする.
- 2 つの要請から変換函數の微分方程式が得られる.
これを解く (実際には数学ソフトを使う).
- 結果は, Schmidt 変換に一致.
|
|
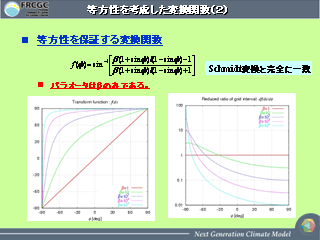
当方性を考慮した変換関数 (2)
- Schmidt 変換
- 等角写像の一種
- 球面から平面に写像し, その像をもう一度別の球へ移す
- βはその球の半径比
|
|
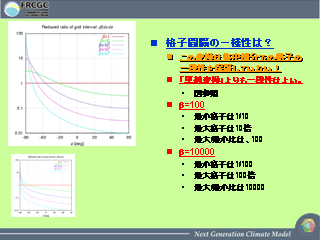
パラメータ依存性
|

|
当方性を考慮した変換関数 (3): β=10
|
|
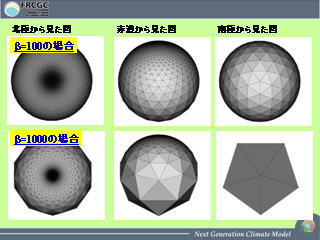
当方性を考慮した変換関数 (4): β=100
|
|
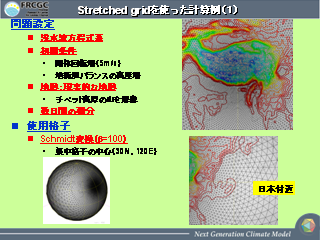
Stretch 格子を使った計算例
- 山を越える流れ
- 球面浅水モデル
- チベット高原の地形データを用いる
|

|
Stretch 格子を使った計算例: 1週間アニメーション
|

|
熱帯スコールラインの実験
|
|
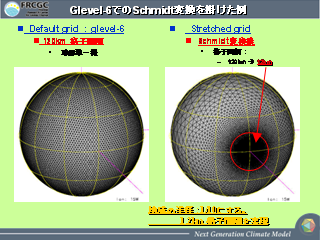
Glevel-6 での schmidt 変換をかけた例
- 半径を 1/10 にしたときに不具合がないか?
- 遠心力項は他の項にくらべるとやっぱり小さいので大丈夫(らしい)
|
|
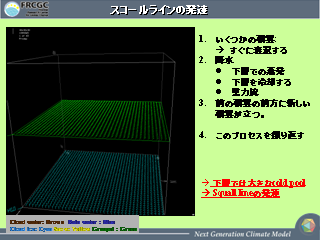
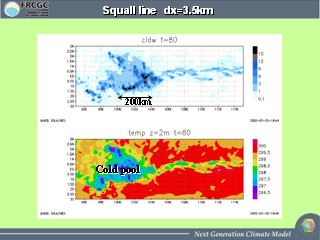
スコールラインの発達
- microphysics のテスト.
- スコールラインちゃんとできる.
|
|
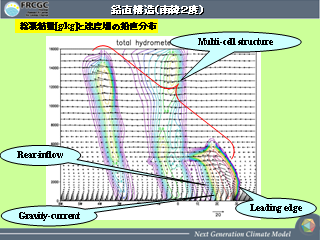
鉛直構造(南緯 2 度): その 1
|
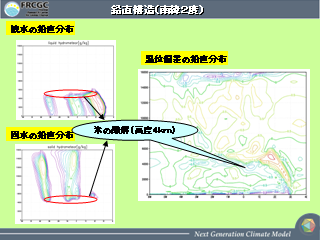
|
鉛直構造(南緯 2 度): その 2
|
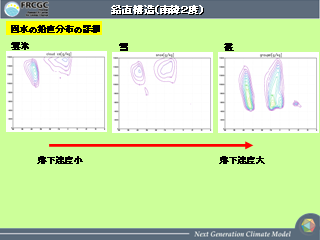
|
鉛直構造(南緯 2 度): その 3
|
|
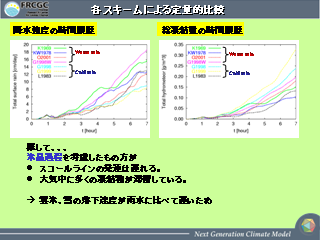
雲物理スキームによる定量的比較
- cold rain スキームの方がスコールラインの発達が遅れる.
|
|
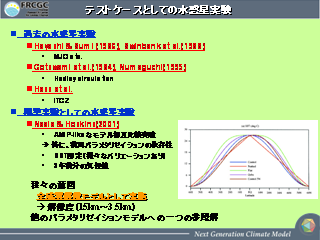
テストケースとして水惑星実験
|

|
Method
|
|
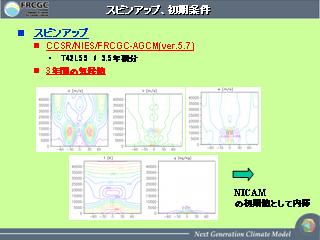
スピンアップと初期条件
|
|
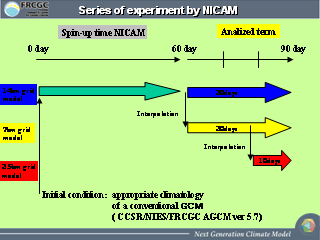
時間積分の実行の流れ
- 3.5km メッシュだと, シミュレータの半分のノードを使って
1 日積分で 5 時間.
|
|
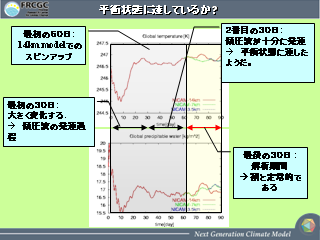
並行状態に達しているか?
|

|
計算結果: 降水強度 [mm/day]
- 3.5 km 格子モデル, 85 日目
- スーパークラウドクラスターが見える
- 中緯度では温暖前線の方が寒冷前線よりもはっきりみえる?
|
|
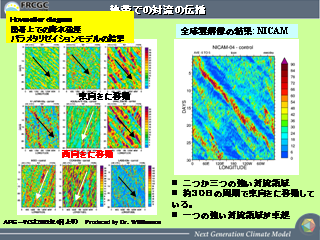
熱帯での対流の伝播
|
|
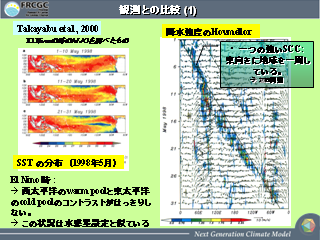
観測との比較 (1)
- El Nino 時の観測された東進する降水強度
- 海面水温分布が水惑星の設定に(気候値に比べると)近いから?
|
|
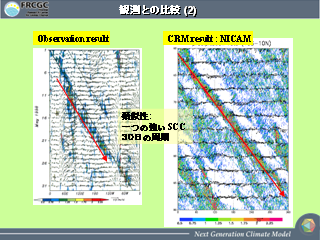
観測との比較 (2)
|

|
ホフメラー図 (7km 格子モデル)
|
|
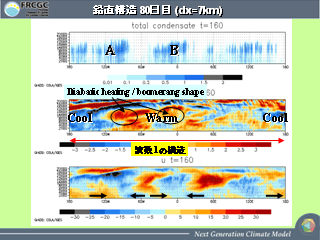
鉛直構造: 7km 格子モデルの 80 日目
|
|
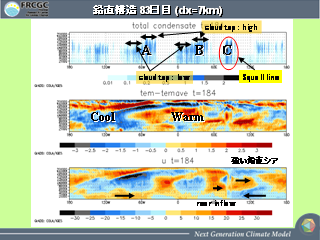
鉛直構造: 7km 格子モデルの 83 日目
|
|
スコールラインの拡大図 (3.5 km 格子モデル)
|
|
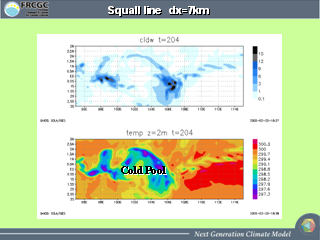
スコールラインの拡大図 (7 km 格子モデル)
|
|
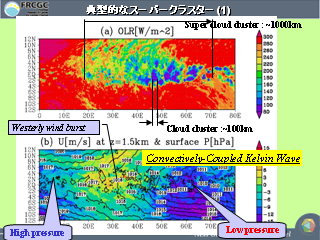
典型的なスーパークラスター (1)
|
|
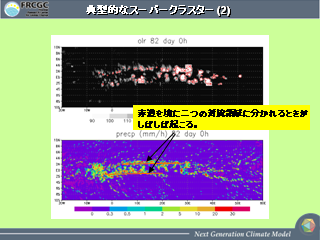
典型的なスーパークラスター(2)
|
|
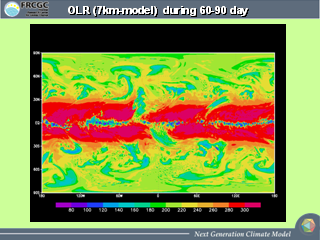
OLR (7km 格子モデル, 60-90 日目)
- 赤道のスーパークラスターから亜熱帯へときどき吹き出しが現れる
- 松野-Gill 応答と考えると吹き出しの場所が合わない
- 用いた SST 分布の影響?
- 観測に比べ, SST の緯度方向への温度勾配が大きい
- 傾圧波動が低緯度よりに出る
- 傾圧波にともなう渦によるひきずり?
|

|
雲イメージ (7km 格子モデル)
- 凝結量の混合比の等値線にボリュームレンダリングしたもの
|

|
雲イメージ (3.5 km 格子モデル)
|

|
スーパークラスターとクラウドクラスター
|
|
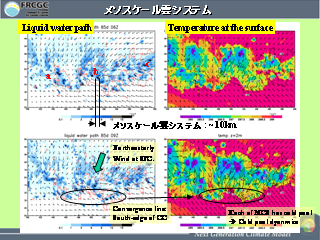
メソスケール雲システム
|
|
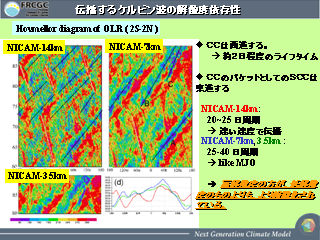
ケルビン波の解像度依存性
- クラウドクラスターは西進
- スーパークラウドクラスターは解像度を上げると遅くなる
- 解像度が高いほどスーパークラウドクラスターの組織化が起こりやすいようにみえる.
|
|
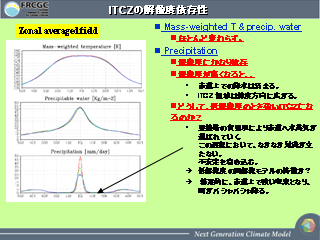
ITCZ の解像度依存性
- 解像度が高くなると ITCZ の雨が弱くなり幅がちょっと広がる.
- 解像度が荒いと雲が立ちにくいから
|
|
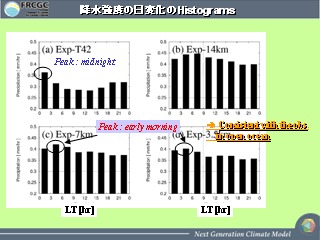
降水強度の日変化の頻度分布
|

|
水惑星実験のまとめ
|
|
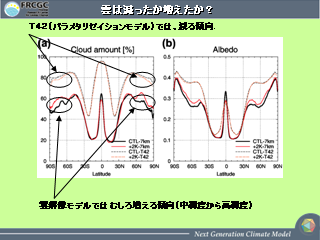
雲は減ったか増えたか?
|
|
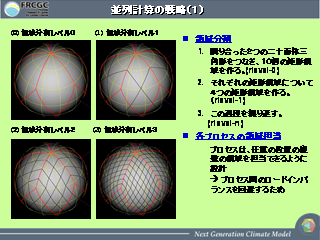
並列計算の戦略 (1)
|
|
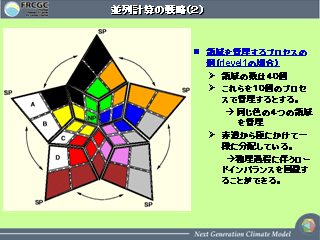
並列計算の戦略 (2)
|
|
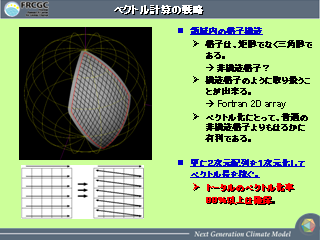
ベクトル計算の戦略
|

|
計算パフォーマンス (1)
|
|
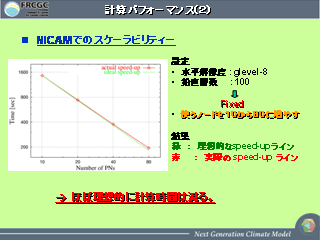
計算パフォーマンス (2)
|
|
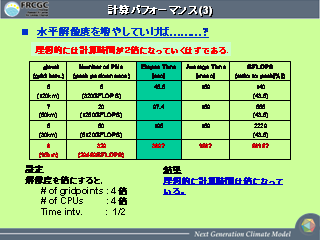
計算パフォーマンス (3)
|

|
計算パフォーマンス (4)
|

|
計算パフォーマンス (4-2)
- AFES の計算時間は n^3 に比例し増加.
-
- NICAM の計算時間は n^2 に比例し増加.
-
- 2-grid scale が最高解像度とすると
- 全ての解像度において NICAM の方が速い.
-
|
|
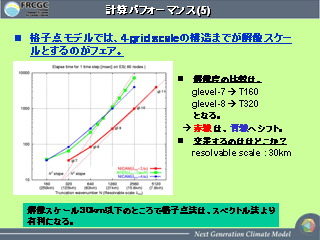
計算パフォーマンス (5)
- 4-grid スケールの構造までが解像されているスケールと考える.
- 4-grid scale が最高解像度とすると同程度.
- T1280 以上では NICAM の方が速い.
解像スケール 30km が境目.
- 普通のやり方(漸化式を使う)だと,
T1200 くらいで Legendre 変換で戻ってこれない.
|

|
計算パフォーマンス (6)
- 目標解像度
L50, Gl-11, Δt=25sec として 320CPU を使うと
1日時間積分で 1:34:10 かかると推定される.
- SR8000 で T42 相当の計算をしたら
CCSR/NIES GCM の 3 倍時間がかかった
|
|
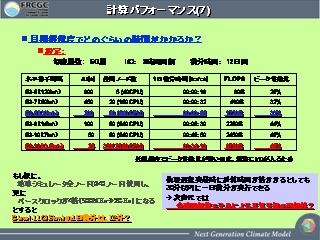
計算パフォーマンス (7)
|

|
まとめ
|
参考文献
- Cote et al., 1998: Mon. Wea. Rev., 126, 1375.
- Cote et al., 1998: Mon. Wea. Rev., 126, 1397.
- Grabowski, 1998: J. Atmos. Sci, 55, 3283.
- Goswami, B.N., Shukla, J., Schneider, E.K., Sud, Y.C., 1984:
Study of the dynamics of the intertropical convergence zone with a
symmetric version of the GLAS climate model.
J. Atmos. Sci., 41, 5--19.
- Hayashi and Sumi, 1986: J. Meteor. Soc. Japan., 64, 451.
- Heikes and Randall, 1995: Mon. Wea. Rev., 123, 1862.
- Heikes and Randall, 1995: Mon. Wea. Rev., 123, 1880.
- Held and Suarez, 1994: Bulletin Amer. Meteor. Soc., 75, 1825.
- Hess, P.G., Battisti, D.S., Rasch, P.J., 1993:
Maintenance of the Intertropical Convergence Zones and the Large-Scale
Tropical Circulation on a Water-covered Earth.
J. Atmos. Sci, 50, 691-713.
- Kessler, 1969: On the Distribution and Continuity of Water Substance
in Atmospheric irculations. Meteor. Monogr., Vol. 10, No. 32, Amer. Met. Soc., 84pp.
- Klemp, J.B., Wilhelmson, R.B., 1978:
The simulation of three-dimensional convective storm dynamics.
J. Atmos. Sci., 35, 1070--1096.
- Nakajima et al., 2000: Geophys. Res. Rett., 27, 3129.
- Neale, R. B., Hoskins, B. J., 2000a: A standard test for AGCMs and
their physical parameterizations. I: The proposal.
Atmos. Sci. Letters, 1, 101--107.
- Numaguti, 1995: J. Atmos. Sci, 52, 1128.
- Lin et al., 1983: J. Climate Appl. Meteor., 22, 1065.
- Louis, 1979: Bound. Layor. Meteor., 17, 187.
- Polvani et al., 2004: Mon. Wea Rev., 113, 2539.
- Satoh M., 2002: Mon. Wea Rev., 130, 1227.
- Satoh M., 2003: Mon. Wea Rev., 131, 1033.
- Swinbank et al., 1988: J. Atmos. Sci., 54, 774.
- Tomita et al., 2001: J. Comput. Phys., 174, 579.
- Tomita et al., 2002: J. Comput. Phys., 183, 307.
- Tomita et al., 2004: Fluid. Dyn. Res., 34, 357.
- Williamson, et al., 1992: J. Comput. Phys., 102, 211.
|
Odaka Masatsugu 2005-09-15
|