/地球流体セミナー
/講演資料一覧
/2003-09-08/
慣性不安定の再考察 :
東西一様な基本場を持つ場合
谷口 博(北大・地球環境)
2003 年 9 月 10 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルページ
|

|
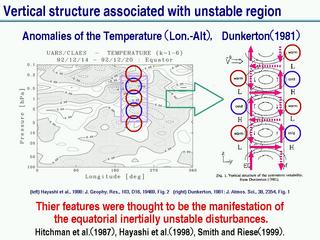
赤道上空で観測されたパンケーキ構造
- Dunkerton (1981) によって予想された慣性不安定構造に似ている.
|

|
これまでの研究
- 理論が先行していたのは以下のようないきさつがあったため(林)
- 大気の「伝統的近似方程式」で 2Ωv cosθ を無視する影響
が問題にしていた人々がいる.
- 海洋の equatorial under current の成因として慣性不安定が考えられていた.
|
|
慣性不安定な構造
- Dunkerton (1981) が構造を理論的に予想.
- 実際に Hitchman et al (1987) が観測で似たような構造を発見.
これは本当に慣性不安定なのか?
|
|
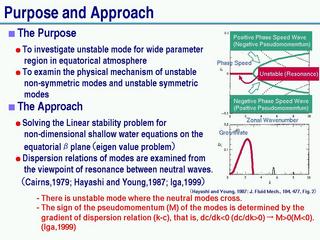
作戦
- 東西一様な基本場での不安定を調べる.
- Hayashi and Young (1987) の方法を利用する.
|
|
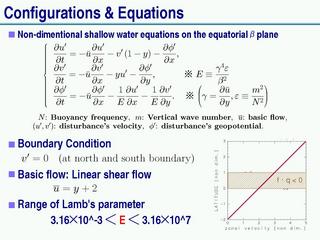
基礎方程式
|
|
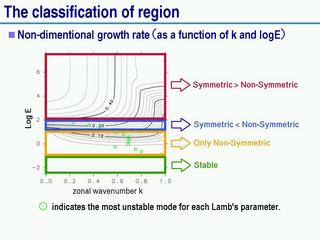
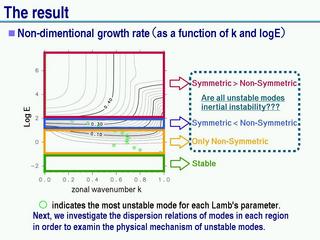
成長率の分布と不安定の分類
|

|
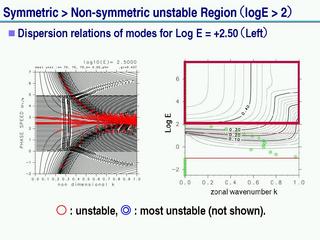
ラムパラメータを連続的に変化させた分散関係
|
|
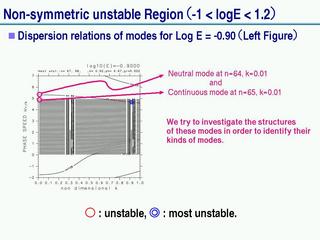
不安定の解析
最初に不安定を起こすモードに注目
- 不安定を起こしていないパラメータ領域での, それぞれの波の構造を調べる.
|
|
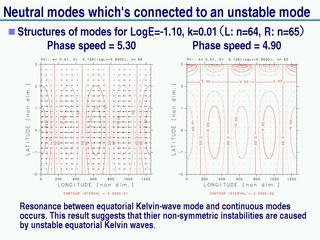
不安定の解析
中立波の構造
|
|
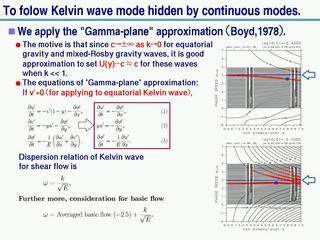
連続モードに隠さた中立波の探索
γ 平面近似を用いる
- Boyd, 1978
- もともとは重力波に対して適用していたもの.
ラムパラメータを大きくしていくと, 数値計算と γ 平面近似解のずれが大きくなる.
|
|
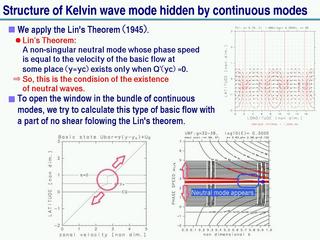
連続モードに隠さた中立波の探索
一部の領域でシアーのない「窓」を開けてみる.
- 中立なケルビン波と連続モードを取り出すことができる場合がある.
- ラムパラメータを大きくすると取り出せなくなる.
- 混合ロスビー重力波とケルビン波の分散曲線が重なるパラメータ値に対応しているようである.
- 渦位 Q を一様にした場合は中立波を取り出すことができない.
|

|
混合ロスビー波 + ケルビン波が重なったパラメータにおける不安定波の構造
|

|
まとめ
|
|
|
参考文献
- Boyd, J. P., 1978:
The effects of latitudinal shear on equatorial waves. I.
Theory and methods.
J. Atmos. Sci., 35, 2236-2258.
- Boyd, J. P., and Z. D. Christdis, 1982:
Low wavenumber instability on the equatorial beta-plane.
Geophy. Res. Lett., 9, 769-772.
- Cairns, R. A., 1979:
The role of negative energy waves in some instabilities of
parallel flows.
J. Fluid Mech., 92, 1-14
- Dunkerton, T. J., 1981:
On the inertial stability of the equatorial middle atmosphere
J. Atmos. Sci., 38, 2354-2364.
- Dunkerton, T. J., 1983:
A nonsymmetric equatorial inertial instability.
J. Atmos. Sci., 40, 807-813.
- Hayashi, Y.-Y. and Young, W. R., 1987:
Stable and unstable shear modes on rotating parallel flows in shallow
water.
J. Fluid Mech., 184, 477-504.
- Hayashi, H., M. Shiotani, and J. C. Gille, 1998:
Vertically stacked temperature disturbances near the equatorial
stratopause as seen in cryogenic limb array etalon spectrometer data.
J. Geophy. Res., 103, D16, 19469-19483.
- Hitchman, M. H., C. B. Leovy, J. C. Gille, P. L. Bailey, 1987:
Quasi-stationary zonally asymmetric circulations in the
equatorial lower mesosphere.
J. Atmos. Sci., 44, 2219-2236.
- Iga, K., 1999a:
Critical layer instability as a resonance between a non-singular
mode and continuous modes.
Fluid Dyn. Res., 25, 63-86.
- Iga, K., 1999b:
A simple criterion for the sign of the pseudomomentum of modes
in shallow water systems.
J. Fluid Mech., 387, 343-352.
- Lin, C. C., 1945:
On the stability of two-dimensional parallel flows Part.II.
Quart. Appl. Math., 3, 218-234.
- Smith, A. K., and M. Riese, 1999:
Cryogenic Infrared Spectrometers and Telescopes for the
Atmosphere (CRISTA) observations of tracer transport by inertially
unstable circulations.
J. Geophy. Res., 104, D16, 19171-19182.
- Stevens, D. E., 1983:
On symmetric stability and instability of zonal mean flows near
the equator.
J. Atmos. Sci., 40, 882-893.
|
Odaka Masatsugu
2003-09-10
|