/地球流体セミナー
/講演資料一覧
/2003-09-08/
シアー不安定の定性的な説明・擬運動量
伊賀 啓太(九大・応用力学研究所)
2003 年 9 月 9 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|

|
固有値問題の解を物理的に理解したい
|
|
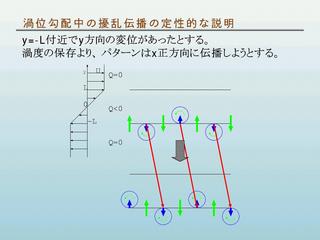
例題:
基本場の渦位境界である y = -L において波形の変移を考える.
- 流体粒子の全渦位が保存されることを考慮して, 擾乱の渦位を考える.
- パターンは x 正方向に伝播
|
|
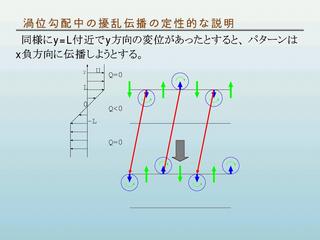
例題:
基本場の渦位境界である y = -L において波形の変移を考える.
- 流体粒子の全渦位が保存されることを考慮して, 擾乱の渦位を考える.
- パターンは x 負方向に伝播
|
|
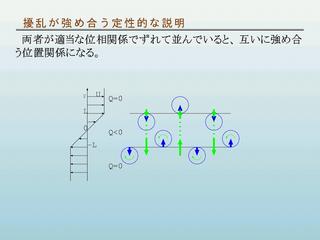
擾乱が強め合う場合の定性的説明
|
|
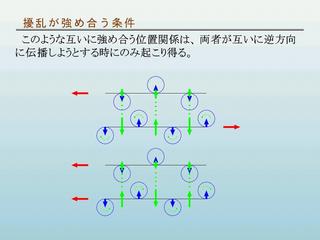
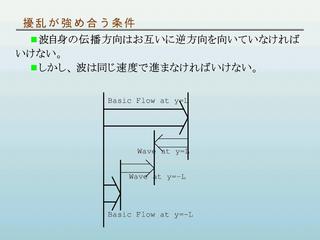
擾乱が強め合う条件
- 互いに逆方向に伝播するような擾乱の組がある場合に強め合う.
|
|
擾乱が強め合う条件 (つづき)
強め合うのに都合のよい位置関係を保つには…
- 擾乱は相対的に逆方向に伝播する.
- 基本場も含めて同じ速度で伝播する.
基本場も含めて同じ速度で伝播しないと, 強め合う位置関係を維持できない.
|

|
不安定が起こるのは…
- 中立波の分散曲線が交わる
- 位相速度はその波が存在する場所の流速の中間値
- 擾乱が振幅が空間的に広がりをもつ場合,
「波が存在する場所の流速」をどう評価するか?
|

|
「その波が存在する場所の流速」をどう評価するか?
- はっきり決められない場合もある
- 別の判定条件を考える : 擬運動量の導入
|

|
擬運動量の導入
|

|
浅水系の擬運動量
|

|
擬運動量の性質にともなう制約条件
|

|
擬運動量が 0 となる場合
正と負の擬運動量を持つ波の対を考える.
- 中立波 : 正と負の擬運動量を持つ波の重ね合わせ
- 不安定波 : 正と負の擬運動量を持つ波がある位相関係を保って存在
- 負の擬運動量を持つ波から正の擬運動量を持つ波へ向かう
擬運動量フラックスがあるとする
- 擬運動量の大きさを強め合う = 振幅を強め合う
|

|
その他の保存量 : 擬エネルギー
|

|
複素共役の和: 擬運動量保存の導出
|

|
複素共役の差: 擬運動量保存の導出
- 擬運動量 × cr な量(擬エネルギー)が存在する.
- 擬運動量は保存量なので, 擬エネルギーも保存量.
|

|
擬エネルギーを用いた解釈
U が一定の場合
浅水系の場合も定義できる.
|
|
|
参考文献
- Drazin, P. G., and W. H. Reid, 1981:Hydrodynamic stability,
Cambridge Univ. Press, pp. 527.
- Satomura, T., 1981: An investigation of shear onstability in a
shallow water. J. Met. Soc. Japan, 59, 148-167.
- Hayashi, Y.-Y., and W. R. Young, 1987: Stable and unstable shear
modes on rotating parallel flow in shallow water.
J. Fluid. Mech., 184, 477-504.
|
Odaka Masatsugu
2003-09-09
|