鉛直乱流混合は Mellor and Yamada (1974)のレベル II の方法を用いている.
Mellor and Yamada (1974)のこの方法は,
拡散係数 ![]() ,
, ![]() , and
, and ![]() は
安定度に依存し,
は
安定度に依存し, ![]() と
と ![]() と
と ![]() の関数として
与えられる.
の関数として
与えられる.
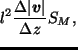 |
(34) | ||
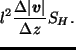 |
(35) |
| (36) |
これらの表現に関して,
![]() と
と ![]() は Richardson 数の関数として与えられる.
は Richardson 数の関数として与えられる.
| (37) | |||
| (38) |
| (39) |
| (40) |
![]() Richardson 数フラックスで, 次のように与えられ
Richardson 数フラックスで, 次のように与えられ
| (41) |
| (42) | |||
| (43) | |||
| (44) | |||
| (45) | |||
| (46) | |||
| (47) |
| (48) |
| (49) |
![]() は次で定義される.
は次で定義される.
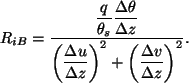 |
(50) |