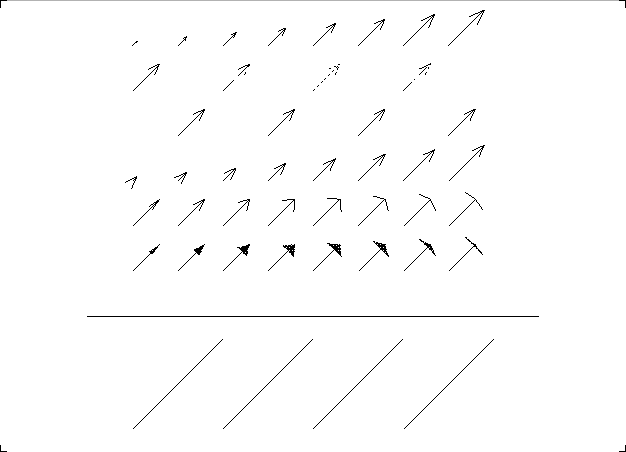
kihonc.f: frame1
プログラム KIHONC で, いろいろな矢印や線分を描いてみましょう. U-座標系での矢印描画は, SGLAU ルーチンで行ないます. 引数は, (X1,Y1) が始点の座標, (X2,Y2) が終点の座標です. 線分の終点から 対称な2本の線分を付け加えて矢じり部分とします. 最初の例のように, デフォ ルトでは, 本体部分が長くなるのに比例して矢じり部分も大きくなります.
PROGRAM KIHONC
WRITE(*,*) ' WORKSTATION ID (I) ? ;'
CALL SGPWSN
READ (*,*) IWS
CALL SGOPN( IWS )
CALL SGFRM
CALL SGSWND( 0.0, 10.0, 0.0, 10.0 )
CALL SGSVPT( 0.0, 1.0, 0.0, 1.0 )
CALL SGSTRN( 1 )
CALL SGSTRF
*-- デフォルト ----
Y1 = 9.0
DO 10 I=1,8
X1 = I
X2 = X1 + 0.1*I
Y2 = Y1 + 0.1*I
CALL SGLAU( X1, Y1, X2, Y2 )
10 CONTINUE
*-- 線分のラインタイプ ----
Y1 = 8.0
Y2 = 8.6
DO 20 I=1,4
X1 = 2*I - 1
X2 = X1 + 0.6
CALL SGSLAT( I )
CALL SGLAU( X1, Y1, X2, Y2 )
20 CONTINUE
CALL SGSLAT( 1 )
*-- 線分のラインインデクス ----
Y1 = 7.0
Y2 = 7.6
DO 30 I=1,4
X1 = 2*I
X2 = X1 + 0.6
CALL SGSLAI( I )
CALL SGLAU( X1, Y1, X2, Y2 )
30 CONTINUE
CALL SGSLAI( 1 )
*-- 矢じり部分の長さ ----
CALL SGLSET( 'LPROP', .FALSE. )
CALL SGRSET( 'CONST', 0.03 )
Y1 = 6.0
DO 40 I=1,8
X1 = I
X2 = X1 + 0.1*I
Y2 = Y1 + 0.1*I
CALL SGLAU( X1, Y1, X2, Y2 )
40 CONTINUE
CALL SGLSET( 'LPROP', .TRUE. )
*-- 矢じり部分の角度 ----
Y1 = 5.0
Y2 = 5.6
DO 50 I=1,8
X1 = I
X2 = X1 + 0.6
CALL SGRSET( 'ANGLE', 10.0*I )
CALL SGLAU( X1, Y1, X2, Y2 )
50 CONTINUE
*-- 矢じり部分のぬりつぶし ----
CALL SGLSET( 'LSOFTF', .TRUE. )
CALL SGLSET( 'LATONE', .TRUE. )
CALL SGISET( 'IATONE', 655 )
Y1 = 4.0
Y2 = 4.6
DO 60 I=1,8
X1 = I
X2 = X1 + 0.6
CALL SGRSET( 'ANGLE', 10.*I )
CALL SGLAU( X1, Y1, X2, Y2 )
60 CONTINUE
*-- ラインサブプリミティブ ----
*-- デフォルト ----
CALL SGLNU( 0., 3., 10., 3. )
*-- 線分のラインインデクス ----
Y1 = 0.5
Y2 = 2.5
DO 70 I=1,4
X1 = 2*I - 1
X2 = X1 + 2.0
CALL SGSLNI( I )
CALL SGLNU( X1, Y1, X2, Y2 )
70 CONTINUE
CALL SGCLS
END
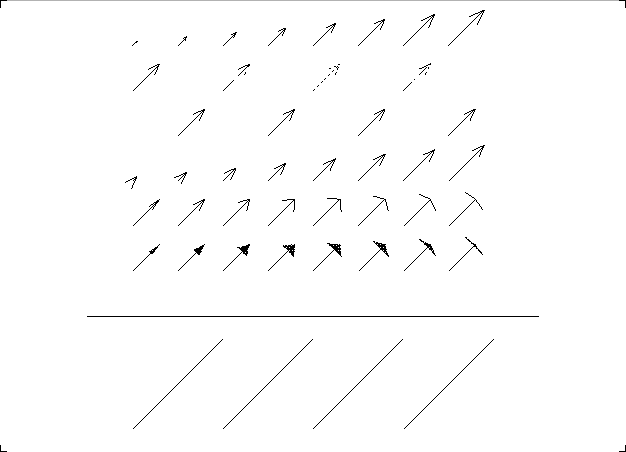
SGSLAT ルーチンでは矢印を描く線分のラインタイプを, SGSLAI
ルーチンではそのラインインデクスを設定できます(2番めと3番め). また,ア
ローサブプリミティブに関する内部変数を設定し直すことにより, 矢じり部分
の形状を変えることもできます. 4番めの例では, 内部変数 'LPROP' を
.FALSE. として矢じり部分の長さが一定値となるようにし, その長さを
内部変数 'CONST' で陽に与えました. さらに, 矢じり部分の線分と本
体部分の線分のなす角を変化させたり(5番め), 矢じり部分を定義する三角形
の領域を塗りつぶしたり(6番め)することにより, 多種多様な矢印が可能です.
最後に, U-座標系での線分描画は, SGLNU ルーチンで同様に行ないます. しかし, これはアローサブプリミティブの特殊な場合(矢じり部分がない場合) と考えられますので, 将来的には削除されるかも知れません.
|